Neural Ordinary Differential Equations (NODEs), Simply Explained

Hello from the AI, but simple team! If you enjoy our content, consider supporting us so we can keep doing what we do.

Our newsletter is no longer sustainable to run at no cost, so we’re relying on different measures to cover operational expenses. Thanks again for reading!

Neural Ordinary Differential Equations (NODEs), Simply Explained

AI, But Simple Issue #75

Deep neural networks have become a cornerstone of modern machine learning, helping advances in fields ranging from image recognition to natural language processing.

Traditional deep models, such as feedforward networks or ResNets, are built by stacking discrete layers of mathematical transformations. Data flows through a finite sequence of transformations, and the depth of the network largely determines its predictive or expressive power.

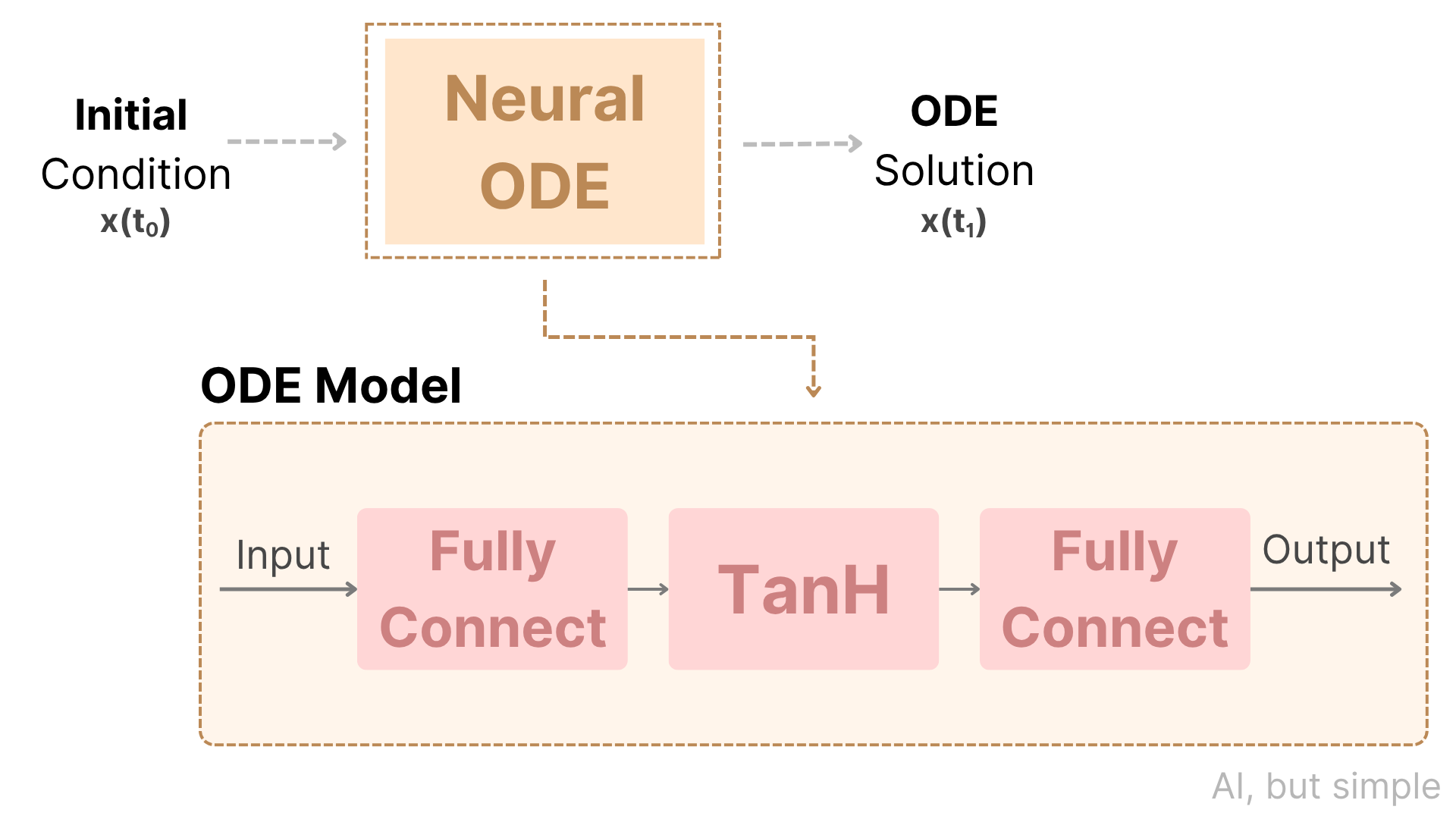
But what if we didn’t have to think of a neural network as a stack of discrete layers? What if, instead, we treated it as a continuous transformation of data over time?

This is the core idea behind Neural Ordinary Differential Equations (NODEs), which is a powerful framework introduced by Chen et al. (2018). NODEs reinterpret the forward pass of a neural network as solving an ordinary differential equation (ODE) parameterized by a neural network.