NRGPT: Combining Energy-Based Models With GPT

Hello from the AI, but simple team! If you enjoy our content (with 10+ custom visuals), consider supporting us so we can keep doing what we do.

Our newsletter is not sustainable to run at no cost, so we’re relying on different measures to cover operational expenses. Thanks again for reading!

NRGPT: Combining Energy-Based Models With GPT

AI, But Simple Issue #88

In partnership with Section:

Transformers for autoregressive language modelling, such as GPT, are typically understood as deep feed‑forward sequence models trained to maximize the probability of correct tokens, which we call maximum likelihood estimation (MLE) in statistics.

While this view has led to extraordinary success, researchers have been exploring new paths for transformer inference, reasoning, optimization, and dynamical systems.

The NRGPT paper (NRGPT: An Energy-based Alternative for GPT https://arxiv.org/abs/2512.16762v1) proposes an energy‑based version of autoregressive Transformers.

• They show that the forward pass of GPT can be interpreted as iterative gradient descent on a learned energy function.

But what is an energy function, and what is energy? How can this be extended to transformers like GPT, and how does it help them reason and choose better answers?

In this issue, we’ll dive deep into NRGPT and the underlying math, categorize it within the broader family of Energy‑Based Models (EBMs), and clarify how it differs from Energy‑Based Transformers (EBTs). 

We will see how NRGPT transforms GPT inference into a stable dynamical system and why this perspective offers a new approach to generalization and reasoning behavior.

A Quick Introduction

Transformer architectures dominate modern machine learning and AI, particularly in language modelling.

Models such as Generative Pre-trained Transformers (GPTs) work autoregressively. This means that they predict the next token given a sequence of past tokens by applying a stack of attention and feed‑forward layers.

In the standard view, each layer performs a deterministic transformation, and inference is a single forward computation through a deep network.

However, recent work has challenged this purely feed‑forward interpretation. Several studies suggest that transformers implicitly perform optimization‑like computations, rather than merely evaluating a static function.

The NRGPT paper makes this idea explicit by reinterpreting GPT as an energy‑based dynamical system, where each layer corresponds to a gradient step that reduces a learned energy.

This perspective is conceptually distinct from prior Energy‑Based Transformers (EBTs), which introduce energy minimization at the output or prediction level.

NRGPT instead embeds energy minimization directly into the hidden‑state dynamics of GPT itself, preserving causality and autoregressive generation.

The AI:ROI Conference – Featuring Scott Galloway and Brice Challamel | Free Virtual Event on March 5

On March 5 from 2–3 PM ET, join Section for the AI:ROI Conference with Scott Galloway, OpenAI’s Head of AI Strategy & Adoption, Brice Challemel, and more.

This is a must-attend session for leaders under pressure to turn AI investment into measurable business impact in 2026. Claim Your Free Spot!

Energy‑Based Models (EBMs)

Energy‑based models define a scalar energy function:

The “R” looking symbol represents the real part of a complex number, as energy must be real.

Here, a low energy (low E) corresponds to preferred or valid configurations. Unlike probabilistic models, EBMs do not require normalized likelihoods.

Inference is performed by solving for the token (value of the input x*) that minimizes the energy.

This is usually done through gradient‑based optimization. In supervised settings, the energy function is parameterized, and energies are conditioned on inputs:

Training encourages low energy for correct outputs and high energy otherwise.

Importantly, EBMs emphasize verification over generation: checking whether a candidate output is compatible with an input is often easier than generating the output directly.

NRGPT leverages this philosophy but applies it at the level of hidden representations rather than explicit outputs.

Standard GPT as a Residual System

Let X^lϵR^nxd denote token embeddings at layer (l). A standard GPT block can be written (simplified) as:

Here, (F) includes causal multi‑head attention, a feed‑forward network, and normalization.

This residual form already resembles a discrete‑time dynamical system. NRGPT makes this resemblance explicit by showing that such an update can be interpreted as gradient descent on an energy function.

How NRGPT Uses the Energy Function

NRGPT postulates the existence of an energy function (E(X)) such that:

Under this assumption, the GPT update becomes:

Which is precisely a gradient descent step with step size η.

The key contribution of the paper is to show that, under mild assumptions on normalization and parameterization, standard transformer components can indeed be derived from such an energy function.

Attention and the Energy Function

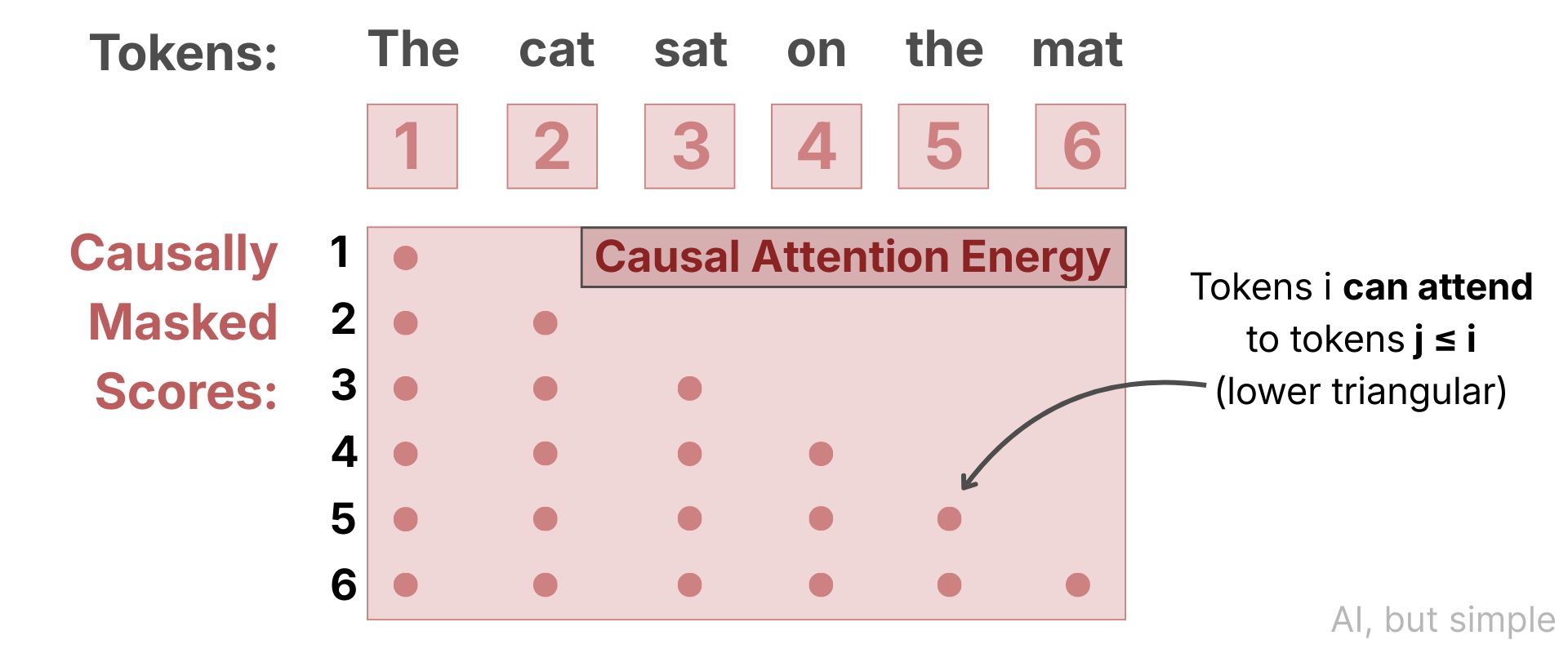
For causal attention, NRGPT defines an energy term of the form:

Above, queries q_i and keys k_j are linear projections of token embeddings. The causal constraint (j < i) preserves autoregressive structure.

Taking gradients of this energy with respect to xi yields attention‑like updates that aggregate information from previous tokens.

Energy For Feed‑Forward Networks

The feed‑forward network (FFN) corresponds to an associative memory energy:

Where ɸ is a learned potential function implemented by an MLP. Its gradient recovers the standard FFN transformation.

The total energy is then:

Weight Sharing and Inference Depth

A defining feature of NRGPT is weight sharing across layers. Instead of stacking different Transformer blocks, NRGPT repeatedly applies the same block:

Here, depth corresponds to inference time, not model capacity. This reframes GPT inference as an iterative optimization process rather than a deep feed‑forward computation.

Stability and Normalization

The paper provides theoretical results showing that, with appropriate normalization (e.g. RMSNorm) and inference‑rate matrices, the energy decreases monotonically after a transient phase:

This guarantees asymptotic stability of inference dynamics. Empirically, even relaxed conditions often lead to stable trajectories, suggesting that training implicitly encourages well‑behaved energy landscapes.

Level Up Your Career With AI, But Simple PRO

Supporting us by purchasing a PRO membership will get you:

• Exclusive Hands-on Tutorials With Code

• Full Math Explanations and Beautiful Visualizations

• Ad-Free Reading for an Uninterrupted Learning Experience

Break into AI or sharpen your edge by joining today!

NRGPT vs. Energy‑Based Transformers (EBTs)

It is crucial to distinguish NRGPT from prior Energy‑Based Transformers.

Energy‑Based Transformers (EBTs):

• Define energies over outputs or predictions

• Perform optimization at inference time to refine predictions

• Often bidirectional or require architectural modifications

• Focus on System‑2‑style reasoning and verification

NRGPT:

• Defines energy over hidden token representations

• Preserves strict autoregressive causality

• Reinterprets standard GPT inference as energy descent

• Emphasizes stability and theoretical understanding rather than reasoning depth

In short, EBTs change what the model predicts, while NRGPT changes how the model computes.

Paper Results

The paper evaluates NRGPT on ListOps, Shakespeare, and OpenWebText. Results show:

• Competitive language modelling performance

• energy‑based version of autoregressive Transformers.

• Increased sensitivity to optimization hyperparameters

These findings suggest that energy‑based inference acts as an implicit regularizer.

NRGPT cleverly bridges transformers, optimization theory, and dynamical systems.

By making inference dynamics explicit, it enables analysis of stability, convergence, and generalization that is difficult in standard GPTs.

Rather than replacing Transformers, NRGPT deepens our understanding of them, revealing GPTs as implicit energy‑minimizing systems.

This insight opens new directions for adaptive inference, stability‑aware training, and theoretically grounded model design.

Conclusion

NRGPT reframes autoregressive Transformers as energy‑based dynamical systems performing gradient descent during inference.

Unlike Energy‑Based Transformers that optimize predictions, NRGPT shows that GPT itself already performs optimization—hidden in plain sight.

This reinterpretation provides both conceptual clarity and a foundation for future work on principled, stable, and interpretable Transformer architectures.

Here’s a special thanks to our biggest supporters:

• Sushant Waidande

• Sai Krishna Pashapu

• Bob Boncella

• Demet Yazici

If you enjoy our content, consider supporting us so we can keep doing what we do. Please share this with a friend!

Want to reach 50000+ ML engineers? Let’s work together:

Feedback, inquiries? Send us an email at [email protected].

If you like, you can also donate to help our team push out better newsletters every week!

That’s it for this week’s issue of AI, but simple. See you next week!

—AI, but simple team